This remarks were delivered on November 8, 2021 when accepting the Hoover Medal at the American Insistute of Chemical Engineers annual meeting in Boston. There is a pdf version available.

It is a pleasure to talk to a roomful of fellow engineers because I’ve spent a career celebrating your creativity. A creativity that, for far too long, we’ve hidden from the public, keeping from view all that’s exciting and enticing about doing engineering. By not clearly sharing with the public what exactly is the engineering method, we dissuade the best and brightest from recognizing engineering as a creative endeavor, which in turn robs us of the next generation of mental firepower which will solve whatever problems our world faces.
So, tonight, I’ll share with you, over thirty minutes, three examples of that creativity that span eight hundred years to lift the veil to show, in all its glory, the engineering method. In these examples of design, which is the defining activity of an engineer, we’ll see the core of the engineering method, how it differs from science, and why it thrives on uncertainty.
We’ll start with what the public often confuses for the engineering method: In their minds, engineering is a subset of the scientific method, the public thinks of engineering as, to use a horrid term, applied science. The only place where the difference is clear is reflected in an old joke: “If it’s a success, then it’s a scientific miracle, if a disaster, then an engineering failure.” This conflation of science and engineering is so pervasive that their differentiation will be appear throughout my talk.
Now, to suggest that engineering practice isn’t subservient to the scientific method likely strikes a counter-intuitive note, after all as engineers we are steeped in science, surely you could not even function as an engineer without science. So, let’s ask “do you need science to engineer something?”

To answer that here’s something designed and constructed by a team of engineers who had never learned science, or even the basic arithmetic and geometry taught today in third grade: Sainte-Chapelle in Paris, built in the mid-thirteenth century. What an incredible design: although the ceiling, arches and pillars are constructed from 400-tons of stone, it isn’t dark like the somber buildings of the Romans in late antiquity. It was by design that the interior fills with light, a hallmark of gothic architecture: Unlike the Romans, these designers used tall pointed arches to accommodate stained-glass windows that transform sunlight into a diffuse red, blue, and gold glow.
To make my point, I could have shown you any of the many chapels and cathedrals built in the Middle Ages — 500 alone in France. All were designed and constructed like Sainte-Chapelle by a team of engineers without scientific and mathematical knowledge. Yet these medieval engineers understood stone structures so well that only a small fraction of cathedrals collapsed in their lifetime of service, and then only after centuries of weathering and neglect after the Reformation compromised them. The design of stone structures like Sainte-Chapelle strips bare the tools often confused for the engineering method – scientific inquiry, mathematical manipulation, computer algorithms, structural analysis, an atomic-level scientific knowledge of construction materials and so on. It exposes what lies at the heart of the method: a surprisingly simple, but rich notion called a “rule of thumb.”
To illustrate that idea, let’s look at how a medieval engineer, more properly called a mason, designed the walls that support safely and economically the breathtaking arches in a structure like Sainte-Chapelle. Key was the correct thickness of the wall supporting the arch: If too thin the weight of the arch would buckle the wall, if too thick, stone would be wasted and the desired open space inside the cathedral diminished. To size the wall, the head mason used a rule inherited from late antiquity, a rule that created the Pantheon and Hagia Sophia: A stable arch results when the supporting wall’s thickness is a little more than a fifth of the arch’s span. But the head mason, though, had likely never learned to read, let alone calculate a ratio, so instead, he did used an emprical method.

He ran a rope along the arch template as if draping the rope over the arch itself — his main task was to create wood templates that were then used by the stonecutters. He then cut the rope to equal the full length of the arch as it curved from the first wall, up to the arch’s peak, and down to the other wall. Then, he folded it into thirds and marked each fold with colored chalk. With the rope now marked into three sections of equal length, he returned it to its original place draped along the arch template. Using the chalk marks on the rope, he could mark two key spots on the arch itself, each falling a short way down from either side of the arch’s peak. He pinned another rope to one of those chalk-marked spots, here labeled “A,” pulled the rope taut to create a straight line from the pinned spot to the point where the arch met its supporting wall, labeled “B” here.
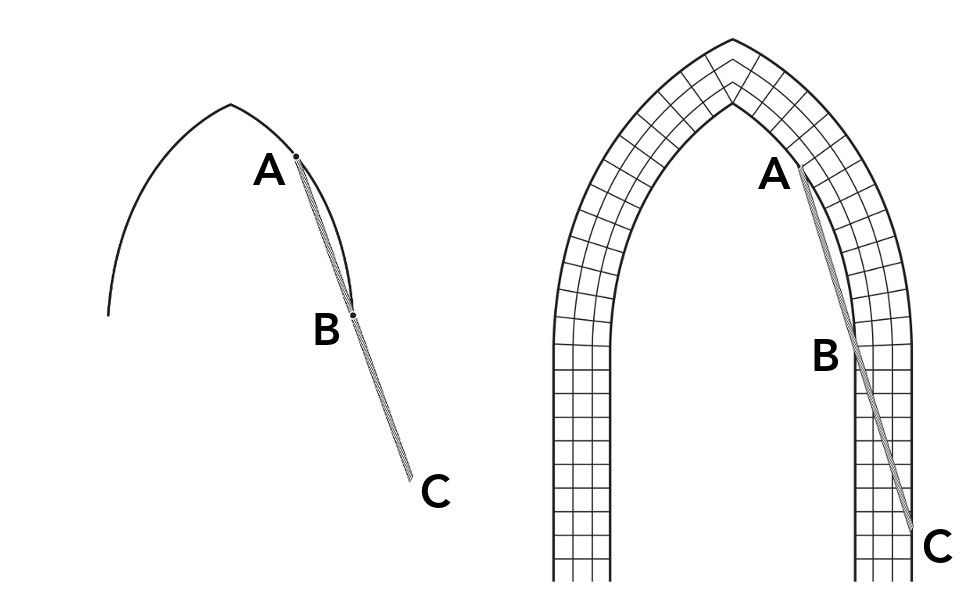
The length of that straightened portion of rope and its particular angle became key, as the mason would then cut another portion of rope of the same length as A-B and lay it, end to end, to extend the path of the taut portion of rope in a straight line — I’ve labeled that B-C here. That extension would become the hypotenuse of a right triangle — though it’s unlikely the mason had heard of either in his life — the shortest leg of which would become his final measurement: the width of the arch’s supporting buttresses. This rule ensured centuries of stability, all without even the simplest mathematical calculation.
This “proportional rule” derived from a thousand years of application and refinement. As more structures stood with dimensions defined by the proportional rule, that rule would continue to be passed on orally and used repeatedly. This rule was one of many that formed a complex body of knowledge known only to head masons — rules that drew on the intuition a mason developed over a lifetime of building.

A “rule of thumb,” otherwise called, more formally, a “heuristic” is an imprecise method used as a shortcut to find the solution to a problem. It is an idea so old and pervasive that practically every language seems to have its own corresponding term, uncannily following a theme of body parts: in French “the nose”, in German “the fist,” in Japanese “measuring with the eye,” and in Russian “by the fingers.” All expressing an imprecise method of guidance by common knowledge, a protocol of estimation. In practice it’s anything that can plausibly aid the solution of a problem, but is not justified from a scientific or philosophical perspective either because it doesn’t need to be or simply because it can’t be justified through anything other than results. Rather than define, it’s best to list the four key characteristics of a rule of thumb.
These four characteristics can be illustrated with a simple rule of thumb used to improve a player’s chess game: “Control the center of the board.”
First, a rule of thumb reduces the time and effort needed to search for a solution to a problem. A player could plan for as many specific game scenarios as possible, but, by generally positioning her pieces to cover spaces in the center of the board, most of those scenarios will be covered without fretting the details.
Second, it can secure a probability of success, but it does not guarantee success. A player who controls the center of the board will not necessarily win every game, but a chess hobbyist who makes a point of doing so will be more likely to win against opponents who ignore this rule. Third, it can remain valid while simultaneously contradicting other rules of thumb that help solve the same problem. A player may also win by remembering to “establish outposts for your knights” or “keep your bishops on diagonals” even while doing so could give up control of the board’s center.
Fourth, it rejects absolute standards. Rules of thumb are designed to be applied and judged according to a problem’s context, but become less useful, perhaps even meaningless, when considered abstractly or objectively. A chess theorist won’t be able to find solid grounds on which to say that “control the center of the board” is any better a rule of thumb than “save your king’s moves for the late game,” and a player might find that every rule they followed before suddenly becomes useless when they try a game of speed chess.
Apply these characteristics to the cathedral’s head mason: First, the proportional rule could size a stable wall in a matter of minutes without spending the time needed to learn the mathematical knowledge to which he lacked access.
Second, although any grand stone structure ran the risk of collapse, he could be reasonably certain that masons throughout history had supported a cathedral with arches designed using the proportional rule, and that his was likely to survive as well. Third, sizing a wall using this rule alone might create too weak a wall, so, the head mason determined the stone’s quality using other rules of thumb that altered the thickness. Finally, these gothic design rules are relative: robust when building cathedrals, but fail catastrophically when applied beyond the construction of medieval stone architecture. If instead an engineer brought back the mason’s proportional rule when designing a skyscraper — a post and lintel structure — it would collapse into rubble under its own weight, likely before even being completed.

Now, I know that it’s tempting to think of the methods of these medieval builders as antiquated, as mere placeholders until the “real” answers arrived in our scientific age. This might lead us to view the mason’s design methods as “protoengineering,” a primitive method that evolved into the sophisticated ones used by modern engineers. But nothing of the kind happened. These proportional rules worked in gothic buildings because the masons never exposed their available and abundant material, stone, to strain anywhere near its failure point, although they never knew this! A stone column will not crush the stones at its base until it reaches 6,500 feet — far higher than the tallest cathedral of the Middle Ages, the 404-foot-tall spire of Salisbury Cathedral. On the right of the figure is silhouette of the cathedral in scale to this 6,500 foot measure. In their time and place, the mason’s rules of thumb were indispensable and insurmountable, but once no longer useful the gothic design rules, instead of evolving, just disappeared. Vanishing both from use and from memory thanks to the oral traditions of medieval apprenticeship. Only in the last fifty years have architectural historians cobbled together these rules using fifteenth-century pamphlets and reverse engineering based on measurements of the cathedrals themselves.
That rules of thumb can be tossed out as easily as they coexist, draws a contrast between the scientific and the engineering methods. The value of a rule of thumb isn’t established by conflict as in scientific theory. Think of Einstein’s theories replacing those of Newton: Newton’s theory was proven wrong and, although revered in history, abandoned by theoretical physicists. The medieval mason’s proportional rule, meanwhile, was never “proven wrong.” That cathedrals are still around today as proof in its favor. It was the material world — the development of iron and steel — that left the rule behind.
Put another way, the scientific and engineering methods have different goals: the scientific method wants to reveal truths about the universe, while the engineering method seeks solutions to real-world problems. The scientific method has a prescribed process that we all learn in school: state a question, observe, state a hypothesis, test, analyze, and interpret, but it doesn’t know what will be discovered, what truth will be revealed. In contrast, the engineering method aims for a specific goal — an airplane, a computer, a cathedral — but it has no prescribed process. The engineering method cannot be reduced to a set of fixed steps that must be followed because its power lies exactly in that there is no “must.” The specialized skill, the defining trait, the great creativity, of an engineer — and what we must show the public — is finding the correct strategy to reach a goal, to select among, and combine, the many rules of thumb that will lead to a solution.
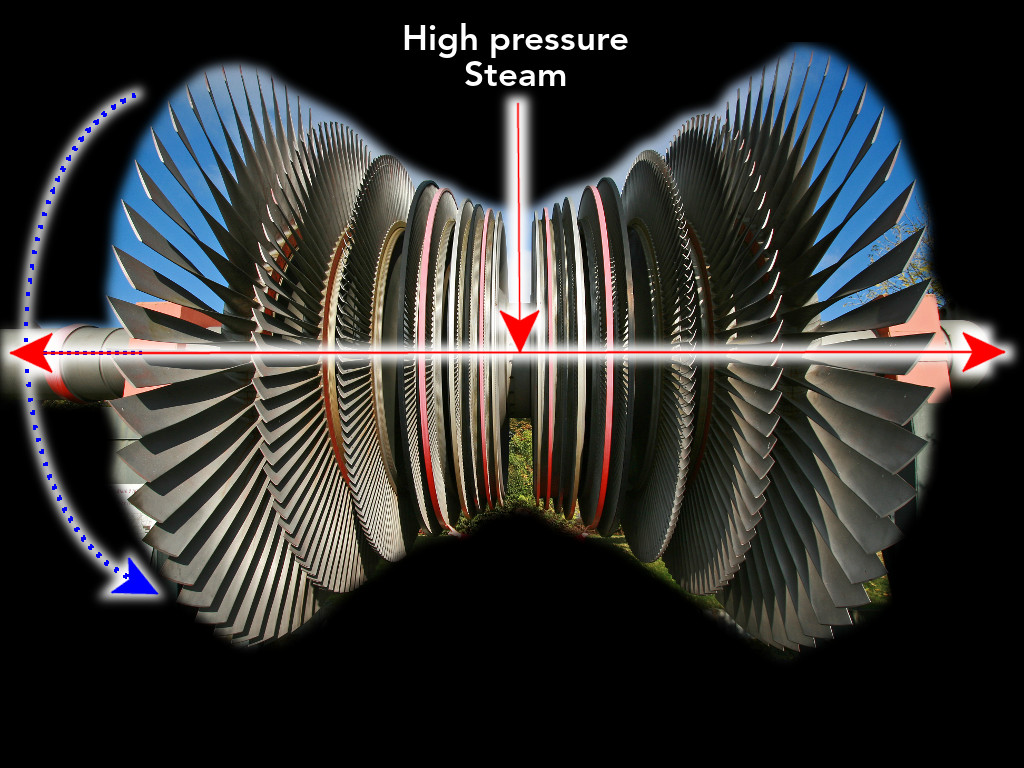
Yet, we teach engineers a lot of science. Which brings me to the true relationship between science and engineering. A relationship illustrated fully by a steam turbine, which I’m guessing is familiar, perhaps even dull, to nearly everyone here: pictured here are the blades and axle of a steam-powered turbine, a ubiquitous device, which generates the vast majority of electricity. Here’s how it works: high pressure stream flows into the turbine, as the steam expands it spins the bladed wheels attached to a shaft — and that shaft spins magnets that generate electricity. Yet, despite its familiarity, few of us know how the interplay of science and engineering produced the first turbine.
A turbine was a dream for thousands of years. To see the engineering problems in creating one, let’s look at two of the earliest devices that use steam expansion to directly rotate a shaft.

One of the earliest was this device, called an aeolipile, designed by Hero of Alexandria in about 130 BC. The ball is filled with water, which when heated turns to steam. The steam blasts through nozzles and spins the device. This device, while delightful — I have one on my desk! — doesn’t have enough power to do much useful. To generate enough torque to drive something like an engine shaft, the steam pressure inside must be many times greater than atmospheric pressure— the higher the pressure of steam, the more it’s compressed, which means it can expand more — but then when released to the atmosphere, high pressure steam would blast from the nozzles at a tremendous 1,200 miles per hour, many times faster than the winds in the most powerful hurricane. At such a speed the device tears itself apart. So, that’s the first problem: the speed of rotation.
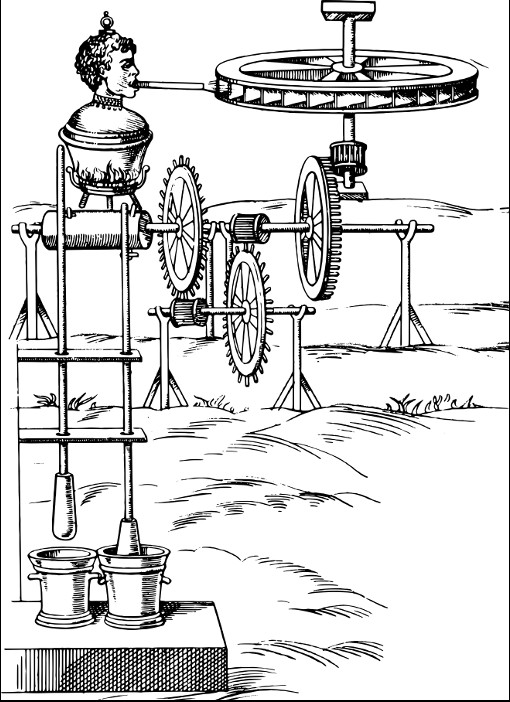
The second method to use steam to directly turn a shaft is shown in this fanciful woodcut from the seventeenth century. In 1629, Givonanni Branca, an Italian engineer, proposed a giant boiler, shaped like a human head, that blasted from its mouth, a jet of steam that stuck a paddle wheel — much like a water wheel — which turned gearing that drove two pestles that pounded mortars. When engineers built devices like Branca’s, not only did the paddle wheel spin so fast that it blew apart like Hero’s device, the high velocity of the expelled steam cut through the metal of the paddle wheel.
For centuries, then these ways of using steam to directly rotate a shaft could not be made to work. In the early nineteenth century in Great Britain, well into their industrial revolution, hundreds of inventors patented steam turbines, all of which failed. Until 1885 when Charles Parsons cracked the mystery of how to tame steam so it could directly rotate a shaft.

To succeed he brought to the problem an astonishing knowledge of steam and steam engines, which he acquired as a child. In the front yard of his childhood home, was, unbelievably the world’s largest telescope, known locally as the “Leviathan.” To give you scale notice that there are three figures at the bottom. Parsons himself is on the right. His father was one of the most important astronomers of the era. For our story, though, it is Parsons’ childhood milieu of machinery and manufacturing that is important. Near the telescope a foundry’s yellow flames lit the grounds at night with an eerie glow as it smelt iron. Surrounding this foundry were workshops filled with lathes, cranes, and glassblowing tools, operated by a team of live-in blacksmiths. Small wonder then that Parsons recalled his childhood as “making contrivances with strings, pins, wires, wood, sealing wax, and rubber bands as motive power, making little cars, toy boats, and a submarine.” But none were more attractive to him than steam-powered motion. Under his father's guidance, Parsons and his brother built, in 1869, a steam carriage that traveled seven miles per hour — a stunning device in an age where the horse remained supreme for several more decades. He never lost this fascination with steam: later in life, as a father, he was always thinking of novel ways to use steam power. For his children he also designed a small car with three wheels and a motor powered by burning rubbing alcohol that chased his children and the family dog around the lawn — his wife banned him from running such toys in the house after a miniature locomotive spit out flaming alcohol, which left a trail of fire on the library carpet. She also forbade him to transport the children in a steam-powered stroller of his design because she feared the cookie tin used as a boiler might explode.
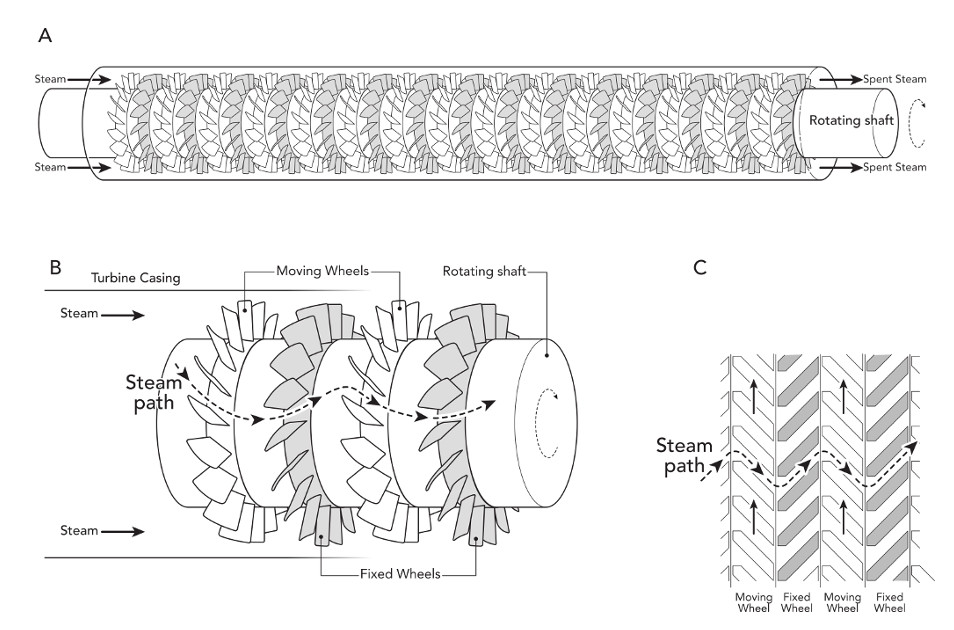
Using his phenomenal machining skill and deep understanding of steam engines from childhood, Parsons created a precise arrangement of thirty bladed wheels on a shaft, which avoided the high speeds that plagued devices like the Hero’s or Branca’s devices. Recall that in those devices high pressure steam inside was allowed to expand all at once to the atmosphere at hurricane speeds, which destroyed the devices. To avoid these problems, Parsons let the steam expand bit-by-bit throughout the turbine. Because of this smaller expansion the steam flowed at a much lower rate than if released all at once; a rate that didn’t cut through the steel blades, and which rotated the wheels more slowly. To give you an idea: if Parsons used one bladed wheel and released all the steam at once, the wheel would spin at fifty or sixty thousands revolutions per minute, but when he released that pressure bit by bit over his thirty bladed wheels the rate slowed to 18,000 revolutions per minute. Now this is still quite fast, and close to twice as fast as today’s turbines, but it was slow enough for Parsons’ turbine to work.
This design is simple in concept, but Parsons himself described the practical problems of executing his design as of “almost infinite complexity.” Think of what he needed to know, or estimate: The number of steps he should use to slowly expand the steam, the speed of rotation caused by the steam’s expansion at each step because he needed every wheel to rotate at the same rate: the device wouldn’t work if this wheel and this wheel spun at different rates because the shaft would be twisted to bits. This meant that he needed to adjust to adjust the spacing between the blades or make them longer to set the wheels’ rotational speed because the steam was expanding as it travelled down the turbine: the spacing between blades is greater and the blades themselves are longer. And lastly, he needed to be sure that at each wheel the stream’s velocity was low enough to avoid cutting steel.
What separated Parsons from the hundreds, perhaps, thousands of inventors before him, was how he navigated his way through this “infinite complexity.” Parsons was among the first engineers to be university-trained, similar to how we train engineers today. So, he turned to what he called the “data of the physicists.” In that data we see the role of science in engineering.

Essential to Parsons work was the information contained in these three volumes: a lifetime of work by the now forgotten French scientist, Henri Victor Regnault, although he was so famous in his time that Gustave Eiffel chose him as one of seventy-two French scientists memorialized on the Eiffel Tower — many names we still recognize today Clayperon, Fourier, Cauchy, Fresnel, Poisson, Le Chatelier, Laplace, Ampere, and Navier. The patient and careful Regnault spent nearly thirty years documenting — as reported in these 3,000 pages — the thermodynamic properties of steam and other substances. All chemical engineers in the room will recognize these as the first steam tables! From the data tabulated here Parsons could determine the volume of steam at every stage of his turbine: that’s how he knew how much to increase the blade spacing as the steam travelled through the turbine.
Regnault’s work helps dispel one myth about engineering and science: that a dramatic scientific breakthrough must precede a revolutionary new technology. I don’t mean to devalue Regnault’s work, but even by the standards of his time it was, well, dull. In his obituary, a prominent chemist eulogized him by saying: “As a scientific investigator, Regnault did not possess the brilliant originality of many of his fellow” scientists. A historian of science described Regnault’s “preoccupation with the tedious accumulation of [experimental] results,” adding that Regnault disliked speculating and discussing theory. Hardly the excitement we associate with a scientific breakthrough. This data alone, though, wasn’t enough, Parsons needed one more thing: how to calculate the velocity of the steam through his turbine.
Recall that the velocity must be low enough not to cut through the metal of the blades, and that it spin the bladed wheels slowly enough that his turbine would not be ripped apart by the rotation. He needed to know how fast steam would travel through the opening between the blades. Parsons’ second scientific resource was the theoretical work of William Rankine, a Scottish scientist and a founder of thermodynamics. In contrast to Regnault, Rankine was anything but diligent, quiet, careful, and conscientious. He was a born performer, as likely to sing at the British Association, the most important scientific meeting in the United Kingdom, as to deliver a paper. Ten years or so after Regnault began his work, scientific papers gushed from Rankine’s desk. These laid the foundation of thermodynamics, although they often built off his idiosyncratic, now forgotten, “hypothesis of molecular vortices.” Of importance to Parsons’s steam turbine was an 1870 paper by Rankine on a phenomenon much simpler than his complex theories of “vortices”: how to calculate the velocity of steam from a nozzle (a small opening) using Regnault’s data. The passage between the blades of the turbine was, of course, a small opening like this.
We see now the two things engineers need from science: high quality data and the some theory on how to calculate with that data. From the combined the work of Regnault and Rankine Parsons knew, and I quote him here, that “a successful steam turbine ought to be capable of construction” because he could now size the number of wheels needed — thirty in his first successful turbine — and he could adjust the blades so that the steam flowed at the same rate through every section. Perhaps not exactly size them because it still took ten years, but it was a starting point that would converge to a successful device.
Parsons’ engineering solution would be impossible without the help of science, which makes his work a paradigm for understanding the relationship between science and engineering. The astronomical number of dimensions and configurations of bladed wheels and every other design variable in the turbine were vast; scientific knowledge helped rule out what wouldn’t work, narrow the possibilities for what does, and shorten the path to a solution. A classic role for rules of thumb. And that is the relationship of science and engineering: scientific practice and knowledge offers engineers gold-plated, grade A, supremo rules of thumbs, rules that work better than those observed merely from observation or long periods of trial and error, yet rules that do exactly what the proportional rule to size a wall did for the medieval mason.
To say “science” created the turbine is to overlook Parsons’ great creativity, his superior machining, and the ten years of trial and error needed to refine the turbine. To call Parson’s work “applied science” is the fuzziest of thinking: it conflates the tool with the method. It’s akin to saying that carpentry is “applied hammering,” that composing music is “applied pitch,” or that writing a book is “applied lettering.”

Whenever we reduce any engineering achievement to one single cause — to the discovery of a scientific fact or even the development of the first working prototype — we hide the rich creativity of engineers from the public. For example, we’re all familiar with the story of Edison and the light bulb: once he discovered the proper filament — carbonized bamboo — the story ends. I know that we all love stories of sole inventors whose spark of inspiration revolutionized the world. They give us narratives that are neat, tidy, and digestible, but incomplete. It hides the engineering method; it conceals the creativity of engineers, smooths over struggles, and sanitizes choice that reflects cultural norms. A technology like a light bulb only solves problems when it can be manufactured or mass produced. A handful of working light bulbs in the late 1800s is a marvel, but it doesn’t light the world. In this sense, the “invention” of the incandescent light bulb is a decades-long process of incremental changes to create a filament that can be manufactured reliably. To tell only a “solitary genius” story shortchanges the contributions of inventive and imaginative engineers who were essential to a technology’s development.

For example, the creativity of Lewis Latimer who devised novel methods to reliably manufacture and assemble carbon filaments. His work was the industry’s standard for the first decade of the commercial light bulb — a critical period that cemented the light bulb as essential — until the carbon filament was replaced by ductile tungsten by William Coolidge — another untold story, yet also an exemplar of the engineering method.
These innovators of the light bulb’s filament, Parsons’ turbine, and the grand structures of medieval builders, leads us to the best definition of the engineering method: Solving problems using rules of thumb that cause the best change in a poorly understood situation using available resources.
That last phrase — “poorly understood situation” — surprises: surely, you are thinking, the stunning advances in scientific understanding and techniques in the previous century and in this century will remove the need for rules of thumb, rules used to overcome uncertainty and to estimate what will happen. Yet, nothing of the sort happens because as scientific knowledge advances, engineers step beyond that knowledge because the purpose of engineering is to solve problems with large degrees of uncertainty. That is the central reason that the engineering method exists.
Consider this last example from the premier science of the twenty-first century: molecular biology. In April of 1953, three papers appeared back-to-back in Nature. These papers lead to deciphering the code of life embedded in DNA, which opened a deep and rich mine of knowledge about how organisms work. To quote a person many in this room are familiar with, Professor Frances Arnold of CalTech, “This code of life,” she said, “is a symphony, guiding intricate and beautiful parts performed by an untold number of players and instruments. Maybe we can cut and paste pieces from nature's compositions.” The idea was that we can ab initio design a biologically-active substance, like an enzyme, because we know this code. The problem with this idea is the complexity of an enzyme. Typically 500 amino acids, of which there are twenty types, are linked to form an enzyme, which means there are 20 raised to the 500 possible combinations of amino acids that can create an enzyme — a mind-bogglingly large number, well beyond the number of atoms in the universe. Finding new and useful combinations among the astronomical possibilities baffled scientists — as Professor Arnold noted of this “symphony” of life, “we do not know how to write the bars for a single enzymic passage.” Yet, as an engineer this did not stop her. She pushed past the boundaries of this scientific uncertainity to create enzymes that reduce the environmental cost of producing our fuels, pharmaceuticals, and chemicals.
Her key insight to overcome this uncertainty was to tap into nature’s own method to create these industrially useful, robust enzymes: evolution. “Nature,” said Arnold, “by far the best engineer of all time, invented life that has flourished for billions of years under an astonishing range of conditions.” By directed evolution she harnessed the nimble, adaptive quality of enzymes and directed it along paths nature left unexplored. Others told her it could not work because nature had already optimized enzymes over billions of years, that any and all useful combinations of amino acids would have been discovered by the immense power of that process, but she realized that this reasoning was faulty: nature had explored only a tiny fraction of life’s molecules, “precisely,” she noted, “because nature did not ask for these behaviors”.

This engineering idea met resistance from scientists. Those who wanted to understand proteins were “aghast,” crying “that’s not science!” She responded by explaining, “I’m an engineer,” noting her goal was the engineer’s guiding principle of “getting useful results quickly.” A classic statement of the purpose of the engineering method! With that key insight Arnold entered the territory most fruitful for an engineer: working on the margins of solvable problems, even those unexplored by nature.
When she accepted the Nobel Prize in Chemistry she said: “A wonderful feature of engineering by evolution is that solutions come first; an understanding of the solutions may or may not come later.” That deep understanding of enzymes has yet to arrive: “even today,” she noted, “we struggle to explain” how her evolved enzymes work. Perhaps the day will arrive when, ab initio, we can design enzymes, but Professor Arnold’s work is a clear reminder that as our knowledge about the universe expands, an engineer will always be out front working in the penumbra of understanding. Because advances don’t remove uncertainty, they simply move the borderline between certainty and uncertainty—the perfect space for an engineer to work.
To lack information, yet design something useful, signals that an engineer is at work. We don’t wait until a scientist thoroughly understands a phenomenon because the public cannot cannot wait for science. In the absence of complete information, engineers for centuries have created buildings, devices, and systems that revolutionize the world — a world full of steel towers, lithium-powered cell phones, ocean-crossing airplanes, life-saving medicine, and spacecraft journeying outside our solar system. All created by the most powerful problem solving method available to humans: the engineering method.
And that brings me to my most important point: The ways in which engineers work their way around that uncertainty must be placed front and center to the public, because that highlights their creativity, ingenuity, and cleverness, and will inspire and entice the next generation of engineers.